三、“对称”是一种变换

    中小学数学教师应该如何认识对称呢？

    下述说法是适当的：对称不是数字，也不是形状，而是一种特殊的变换（transformat ion），一种移动物体的方式。换言之，若一个物体在经过变换之后看起来与之前相同，那这个变换就是对称。简言之，对称是个变换，这个变换的功能是“保持不变”。 

    如果忘了中学或大学所学，对“变换”一词的数学含义记不清了，没关系！换成“操作”这个词也行，“变换”就是“操作”。如果对“物体”这个词也感到困惑，认为有设限之俗，有悖“君子不器”，那干脆把“物体”这个词也省掉，于是就有了“对称”的一个简化版表述：“对称就是操作后不变”。 

    问题又来了，谁是操作者？这么问导致的麻烦是有可能列举不尽操作者，那还不如不问，多一事不如少一事是数学研究者的工作风格。不提并不意味着不存在，反正数学家兼哲学家罗素（B ertand Russell）曾经说过：数学可以界定为不知道在说什么，也不知道说得对不对的学科。这个深不见底的名言透露出数学其实并不喜欢把什么都搞清楚说明白，数学是 “难得糊涂”的典范，数学之如此反而给自己留下了巨大的话语空间。这里，数学之聪明表现为：既然不提这个事于大局无碍，那就不提为好。待碰到具体问题需要搞清楚操作者是谁的时候，再说！

    譬如看到有蜜蜂进出的窝是如图1所示的六角形对称结构，若问谁建的，谁是操作者，答案自然是蜜蜂，是它们构造了蜂巢（图1表达的是蜂巢六角形窝洞底部封口的结构）。瑞士数学家克尼格曾经计算过，若要消耗最少的材料来制成最大的菱形容器，其六角形的钝角角度应该是109º26′，这比法国人马拉尔第测得的蜂巢六角形的钝角角度109º28′要少2分。但之后苏格兰数学家马克劳林重新计算证实了：蜜蜂是对的，克尼格的计算是错的。蜂巢是精密的对称性建筑，精明的蜜蜂们为了用最少的材料来制成最大的菱形容器而自然选择了精准的角度，并做到了一分不差。伟大的操作者——蜜蜂！

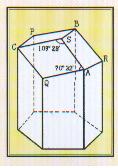
图1

    科学家发现，蜂巢的一头是正六边形，另一头被3个相同的菱形密封住。17世纪，法国天文学家马拉尔第测出蜂巢菱形的纯角是109º28′，锐角是70º32′。18世纪，瑞士数学家克尼格算出用最少的材料做出最大的菱形容器，钝角应为109º26′、锐角应为70º34′。苏格兰著名数学家马克劳林（1698-1746）重新计算得到的结果是109º28′和70º31′44″。克尼格之错缘于他用的数学用表印错了。

 

    守恒与永恒同义，是自然科学致力于揭示的自然规律。据说公认的守恒律共有12个，力越强，其交互作用越受守恒律限制。强相互作用力交互作用受所有12个守恒律的限制，电磁力交互作用受11个守恒律的限制，弱相互作用力交互作用受8个守恒律的限制。引力受哪些守恒律的制约，至今还处在探索中。这些守恒定律中，大家最熟悉的莫过于质量守恒定律和能量守恒定律。

    爱因斯坦说“能量拥有质量，质量就是能量”，口说无凭，他还给出了这个说法的数学表达E＝mc2。人类与地球、太阳、银河系共处于时空中，受时空规律左右，而时空守恒定律揭示的是万物生成和运行的规律，不变或永恒是“对称”的本质，所以人们把守恒律也称为对称律。如果一定要问时空对称的操作者是谁，人类拟就的答案有很多，甚至宗教信仰都有可能在其中发挥影响，于是，对时空的解释也存在远离规律或事实的可能。

    前面提到小学生或者大多数人对“对称”的理解是基于特定形状的，是某些规则形状使然。而变换意义下的对称说的是：如果某物形状被旋转后没有发生形变，与原形状无异，则称旋转前后的两个形状是旋转对称。仔细想想，这太令人吃惊了，“对称” 竟是这样的普遍存在，一个东西挪个窝、转个圈，只要不因此有毫发之损之变，就相当于进行了一次对称变换。

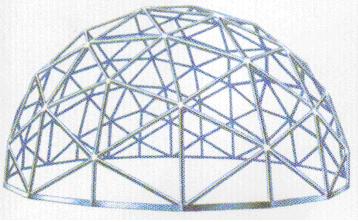
图2

这个网格半球体建筑可以表达多种含义的对称形状。
 

    例如图2，这个网格半球上的三角形们是全等的，可以看作是一个三角形在球面上运动的结果。虽然这个网格球体不是严格意义上的球，但这岂不是说平面上凡具有全等性质的图形，或空间中凡具有全等关系的实体，本质上是一个图形、一个实体位移的结果？是这样的！全等意义下的图形只有一个，这是对称的意义之一。

    这方面最典型的、也为学生最熟悉的对称形象是圆，圆是完美对称的典范，其数学表达也极其简单。公元前580年，希腊哲学家阿那克西曼德（Anaximander）因所有形状中最对称的是圆形而给出了第一个宇宙模型，自此圆形统治天文学一直到1609年，这年开普勒证明了火星运行轨道是椭圆。

    圆，无论怎样转动她，都不会变形，都看不出转与不转的区别。

    但令人困惑的是，并非看着完全相同的事物，或者说是左右对称的事物，经过旋转和平移，他们就可以重合。如图3，若为飞机机身画一个左机翼，再对称画一个右机翼，不难发现：只要不脱离纸面无论怎样平移或旋转，左机翼都无法与右机翼重合，除非左右机翼翼型是经过平移或旋转能够重合的特殊形状，例如矩形、等腰三角形、等腰梯形等。

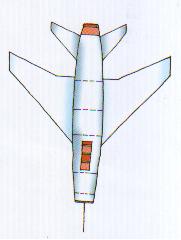
图3

    若不翻折，在平面上你无法使左机翼与右机翼重合。这其中暗含着一个事实。二维平面上无法办到的事，在三维空间中可以办到。譬如使左右机翼重合。
 

    于是镜像对称（亦称“反射对称”）概念就成为必要的了。我们可以通过空间翻折（翻筋头）来达到左右重合，来说明左右机翼是镜像对称的。

    有意思的是，人们比较认可镜像对称图形的对称性，而对于更具普遍性的平移对称现象，反而往往忽略其对称属性，例如图4所表达的平移对称。典型的实例是工厂流水线末端的产成品，它们就是平移对称的。批量生产产品的思想本质上是对称概念的实际应用。另外，假如你试图用重合法来证明自己的左右手是对称的，不妨想想能否做到，若不能做到，能琢磨出一个解决方案来也是不错的！

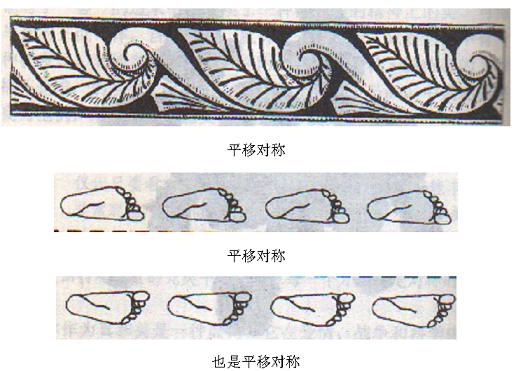
图4