湖南省常德经济技术开发区莲花池小学 刘婷婷老师上出数学示范课
 

    【摘要】在新课程实施中，如何在日常教学中将打好“双基”和“创新设计”结合起来，是教师教学的难点 。

    通过一系列的创新点设计案例，探讨教师在日常教学中设置创新点，以较低的教学成 本提供创新思考”的空间，培养学生数学创新能力的方法。

    【关键词】数学教学；探究学习；教学设计

    我国数学教学的长处是注重“双基”，弱点是“创新”不够。因此，一段时期以来，如何进行探究性教学、研究性学习受到广泛关注。但如果探究课需要占用大量时间， 缺乏教学效率， 教学成本太高，则只能偶尔为之。

    这就为我们提出一个研究课题，在日常教学中， 教师如何将打好“双基”和“创新设计”结合起来。

    以往的教案编写都要写教学目的， 指出重点和难点。这就启发我们， 可在教案中加入“创新点”的设计， 即用较短时间，因势利导地提供“创新思考”的空间。这样， 画龙点睛， 长年积累，形成创新的思维习惯，最终可以提高学生数学创新能力。

    让我们先看一个案例【1】。这节课的内容是七年级上册“同类项概念”的教学。

    教师首先按常规复习多项式的“式”、“项”和“次数”的概念。按惯例，教师会接着把同类项的概念写在黑板上，然后给出很多单项式, 让学生判别它们是否是同类项，进行模仿练习。

    然而我们也可以用设立创新点的教学设计，启迪学生的探究、创新思维。于是，教师在黑板上写下一个多项：

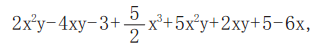
并提问：“我们常常把具有相同特征的事物归为一类。在多项式的各个项中，也可以把具有相同特征的项归为一类，你认为上述多项式中哪些项可以归为一类？为什么？”以下是学生的探究。

    学生甲：一、二、四、五、六、八项可归为一类，因为都含有字母。另外， - 3 、+ 5 为一类，它们都是常数。

    学生乙：一、二、五、六项为一类，它们都含有两个字母x 、y ；5/2x3、- 6x 为一类，这两项只含有一个字母；此外，- 3 、+ 5 都是常数项，同为一类。

    学生丙：一、四、五、六、七项为一类，因为它们的分数为正数；其他的一类数为负数。

    学生丁：一、四、五项为一类，因为它们的指数为3 次。
    ……

    学生的各抒己见，着实令人欣慰。他们用数学的基本概念对单项式作了分类，符合“具有相同特征的项归为一类”这一要求。这样的“探究”，是数学分类思想的一次很有意义的实践。然而，这些答案都没有涉及“同类项”的本质，还不能得到同类项的概念。

    于是，教师继续设置第二个探究点，再提出两个问题：“( 1 ) 如果不考虑项的系数，只考虑字母怎么分？( 2 ) 如果还考虑字母的指数又怎么分？”新的问题使学生的反应更加热烈，连平时不爱动脑发言的学生都纷纷举手发表“自己”的见解。这节课气氛很活跃，最终朝着我们希望的方向发展下去，效果很好。

    这样的设置并没有花费太多时间，却达到了探究目的，使学生在数学分类思想指导下，用自己的思考得出同类项的概念。对学生来说，这就是创新。

    由这一案例可见，创新点设计并不神秘。这样的方法，许多教师也常用。例如，教师创设情景让学生归纳猜想；教师提供问题让学生寻求解法(包括一题多解)；教师提供案例让学生反思获得“数学思想方法”等。

    创新点设计的要求是经常使用，每堂课都用，成为日常的教学手段。我们需要的是通过系列化的研究，日积月累，培养学生的创新能力。

    数学教学中的创新点，要从两方面进行设计：一是数学内容要“新”，要求学生在数学上经过思考有所探索、发现；二是教学过程中要“创”，教师要有意识地为学生设置思考空间。至于创新形式是多种多样的，可以是学生独立思考，进行归纳猜想、尝试求解、发散开放、推广发现、合作讨论；也可以是教师有目的地提问，采用启发式方式和学生对话。甚至教师做创新的示范，也可以作为“创新点”加以设计。

    我们再举以下教例说明“探究创新点”的教学设计。

    例1：“对顶角相等”的教学

    通常按照教材，用对顶角的补角相等加以证明，让学生模仿证明的格式，就完成了教学。这时，如果教师提问：“这样明白、浅显、直观的数学命题为什么需要证明？”这个问题就是有关“培养学生理性思维的探究点”。

    通过师生探究讨论，使学生理解古希腊文明的价值，也给学生理解几何证明提供了人文思考。这也是数学教学中德育功能的体现。

    例2：“方程概念”的教学

    通常是把教材中方程的概念直接加以叙述：含有未知数的等式叫方程。然后， 写出很多式子，看看是不是“方程”。这个定义其实没有科学价值，学生无需记住，也没有应用。为了设置探究点，教师可以从“小明的爸爸今年42岁，比小明大30 岁，问小明几岁”出发。

    于是，教师列出等式：小明爸爸年龄－小明年龄＝30 已知数( 42 )－未知数＝30未知数＝12

    以上过程就是解方程。因此，方程是为了寻求未知数，在未知数和已知数之间建立的等式关系。可以让学生讨论哪一个定义更好。学生探索之后悟出：书上的方程定义，是外观的描述；而后者的定义则刻画了方程的深刻本质。这样的探究点设计，更能引发学生的创新思维。

    例3：“勾股定理”的教学设计

    最近看到许多“探究性”的勾股定理教学设计，都把重点放在事先的发现上。学生拿到多张工作单，从最简单的边长为3 、4 、5 的直角三角形开始，直到最后“探究”出a2+ b2= c2的公式。这种设计费时很多，收效不大，原因是“发现”定理的教学成本太高。

    如果采用其他探究设计，如一开始就用多媒体技术介绍勾股定理的历史，直接呈现漂亮的“勾股定理”本身，而把探究重点放在“证明”勾股定理上，就会节约时间，更接近论证教学需要。

    可将探究重点放在以下三种证明方法的比较：面积拼凑法( 出入相补原理)，面积计算法( 赵爽)，补助线演绎证明法( 古希腊)。这样的探究设计，具有更多的数学价值。

    例4：“对数性质”的教学

    通常我们总是从指数的逆运算引入对数，然后指出对数的性质是把数的乘法变换成加法，这当然是对的。但仍然是这些内容，我们却可以以更高的数学思想方法进行设计，这就是徐利治先生提倡的RMI 方法。对于a ≠1

这是指数函数构成的对应关系。现在，我们把箭头反过去，它也是一个对应，即函数。那么这个函数具有什么性质？

    这样提出问题，就首先考查函数应有的性质，然后给它一个名称——对数。实际上，这样设计并没有增加学生的额外负担，内容还是原来的内容，教学时间依然和原来一样，但是具有探究的味道，这就是可以日常使用的创新点。

    例5：“负负得正”的算法规定

    这是有理数四则运算的一项重要规定。它无法证明，又没有世人所公认的好例子可以作为规则成立的背景。

    近来教科书使用的方法，是用实际例子创设情景(例如设定火车向东为正，时间12时以后为正，然后硬编出一个大家都不熟悉的怪问题)，企图让学生“发现”负负得正的规则。实际的教学结果只是把学生搞得头脑混乱，浪费时间。

    我们不要让学生去“发现”负负得正的规律，因为那是短时间内发现不了的。世界上还没有发现一个为大家普遍接受的“负负得正”的实际情景。因此，我们不得不采用接受性的教学策略，即直接告诉学生：“根据前人的经验，负负得正是一个大家都认为应该遵循的规则。”

    这节课的教学目的在于：能够熟练操作、准确执行“负负得正”的规则。至于这个规则的来龙去脉，不必深究，一般学生只要接受“负负得正”，不抵触就行。

    那么，这一内容的探究点在哪里呢? 一种教学设计是：“大家给它作解释，而每人可以不一样。”以下是大家探究的各种解释。

    第一种解释：某数乘以- 1 得到它的相反数，再乘- 1又返回到自身，所以- 1乘以- 1等于+ 1 。这就是负负得正。

    第二种解释：满足分配律。例如按照分配律，应该有：- 5 ×( 4 - 2 ) = ( - 5 ) ×4 + ( - 5 ) ×( - 2 )左端是( - 5 ) ×2 = - 10；右端的第一项是- 20，所以两个负数相乘的第二项必须是+ 10，才能两边相等。这解释了负负得正的运算规则。

    第三种解释：符合运算结果的对称性。例如：
    ( - 2 ) ×2 = - 4
    ( - 2 ) ×1 = - 2
    ( - 2 ) ×0 = 0
    ( - 2 ) ×(- 1 )= 2
    ( - 2 ) ×(- 2 )= 4
    还可以有多种解释。这些解释都不是证明，也没有好坏之分，只要学生能够说服自己就行。实际上，学生掌握“负负得正”的运算规律之后，就把这些解释忘掉了。

    从以上例子可以看出，探究创新点无处不在，基本类型有：

    1．通过教师提问，为学生预留思考的空间，促进学生思维的开放。如本文所举的样例，又如一题多解，让学生尽量提供较多的不同解法。

    2．通过教师创设情景，要求学生归纳猜想，建立数学模型，借助数学的各种呈现方式进行比较，得出新的结论。这是目前情景创设教学常用的。

    3．通过教师示范，展示创新的过程；或者介绍数学家创造数学的历史，激励学生的创新动力。如例1“对顶角相等”的教学。

    4．通过设置数学教学平台，让学生认识数学的教育形态，把书上的学术形态情景化，暴露它的数学实质。如例2“方程概念”的教学。

    5．跳出“事事发现”的误区，把探究点放在“反思”求证阶段，如例3 “勾股定理”的教学设计。

    6．通过适当的问题，让学生总结数学思想方法，由感性的体验上升为理性的思考，理解数学的本原。如例4“对数的性质”教学。

    7．通过教师与学生的互动，交流数学学习的体会，如例5 “负负得正”的算法规定，把接受性学习探究化。

    8．欣赏数学的美，体会数学的人文价值。如例3“勾股定理”的教学设计，注意该定理的美，以至将它作为和外星人通信的文化载体。

   [ 注释]
   [1 ] 本案例由宁波福明中学黄美珍提供。
   [ 参考文献]
   [1 ] 范良火等著, 唐瑞芬等译:《华人如何学习数学》, 江苏教育出版社, 2005 年版。
   [2 ] 张奠宙编:《中国数学双基教学的理论与实践》, 上海教育出版社, 即出。
   [3 ] 张奠宙、宋乃庆主编:《数学教育概论》, 高等教育出版社,2004 年版。

   （重庆市大渡口区实验小学 刘 凤老师推荐）